3.3. Spherical coordinates

There are several possible coordinate systems that can be used to define a location in three-dimensional space. Besides the Cartesian coordinates \((x,y,z)\), one can use spherical coordinates.

Definition

In spherical coordinates, a point is specified by three coordinates:

  • \(r\): the radial distance, i.e. the distance of the point from the origin

  • \(\theta\): the polar angle, i.e. the angle down from the \(z\) axis, limited to the range 0 to \(\pi\)

  • \(\phi\): the azimuth, or azimuthal angle, i.e. the angle off the \(x\) axis in the \(xy\) plane, limited to the range 0 to \(2\pi\)

Figure 3.21 illustrates these coordinates and how they are related to the Cartesian coordinates

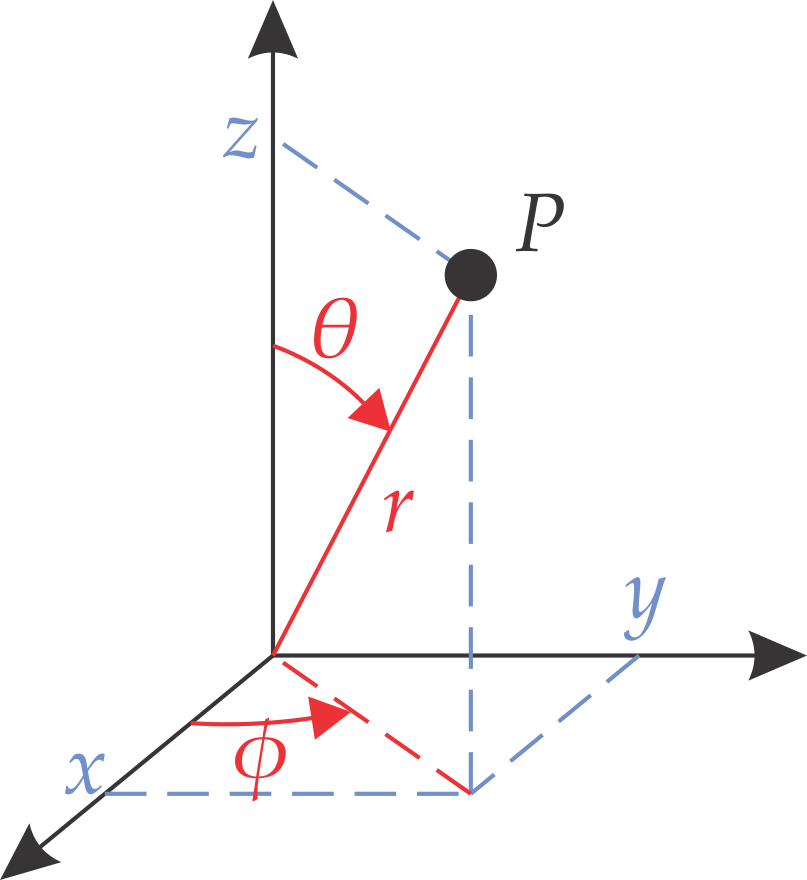
_images/math_sphericalcoordinates.png

Figure 3.21 The Cartesian coordinates (blue) and the spherical coordinates (red) of a point \(P\).

This is the definition used in quantum theory and physics. Other fields (mathematics, etc.) use different definitions.

Conversions

The conversion from spherical coordinates to Cartesian coordinates is as follows

(3.46)\[\begin{split}\begin{align} x &= r \sin\theta\cos\phi \\ y &= r \sin\theta\sin\phi \\ z &= r \cos\theta \end{align}\end{split}\]

To convert from Cartesian to spherical coordinates, use

(3.47)\[\begin{split}\begin{align} r &= \sqrt{x^2+y^2+z^2} \\ \theta &= \arccos(z/r) \\ \phi &= \arctan(y/x) \end{align}\end{split}\]

Integral

Integration of a function \(f(r,\theta,\phi)\) over all space in spherical coordinates requires

(3.48)\[\int_0^\infty \int_0^{2\pi} \int_0^\pi f(r,\theta,\phi) \cdot r^2\sin\theta \, \mathrm{d}\theta \mathrm{d}\phi \mathrm{d}r\]

Do always include the factor \(r^2\sin\theta\).

Laplacian

The Laplacian \(\nabla^2\) in spherical coordinates is the sum of a radial operator \(R^2\) and an angular operator \(\varLambda^2\)

(3.49)\[\nabla^2 = R^2 + \frac{1}{r^2}\varLambda^2\]

The radial operator has several equivalent forms

(3.50)\[R^2 = \frac{1}{r^2} \frac{\partial}{\partial r} \left(r^2\frac{\partial}{\partial r}\right) = \frac{\partial^2}{\partial r^2} + \frac{2}{r} \frac{\partial}{\partial r} = \frac{1}{r} \frac{\partial^2}{\partial r^2} r\]

The angular operator is

(3.51)\[\varLambda^2 = \frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\theta\frac{\partial}{\partial\theta}\right) + \frac{1}{\sin^2\theta} \frac{\partial^2}{\partial\phi^2}\]

The angular-momentum operators used in the description of rotating molecules and in the Hamiltonian for the hydrogen atom are proportional to \(-\varLambda^2\).