Coordinate frames in EasySpin

To simulate EPR spectra, EasySpin needs to know about the relative orientations of the various tensors within a spin center or paramagnetic molecule, of the molecule within a sample such as a crystal, and of the sample within the spectrometer in the lab. For this purpose, EasySpin defines a set of cartesian coordinate frames. Specify the relative orientation between these frames in order to describe the geometry of your sample and your experiment.

The figure below summarizes EasySpin's frames. There are four frame types: the lab frame, the sample/crystal frame, the molecular frame, and a set of tensor frames (one for each tensor). The orientation of the sample (crystal, film, powder, frozen solution, etc.) in the lab frame is given in Exp.SampleFrame, the orientation of the paramagnetic molecule in the sample frame is given in Exp.MolFrame, and the orientations of the various tensors in the molecular frame are given in Sys.gFrame, Sys.AFrame, Sys.DFrame, Sys.QFrame, Sys.eeFrame, Sys.nnFrame, and Sys.DiffFrame.

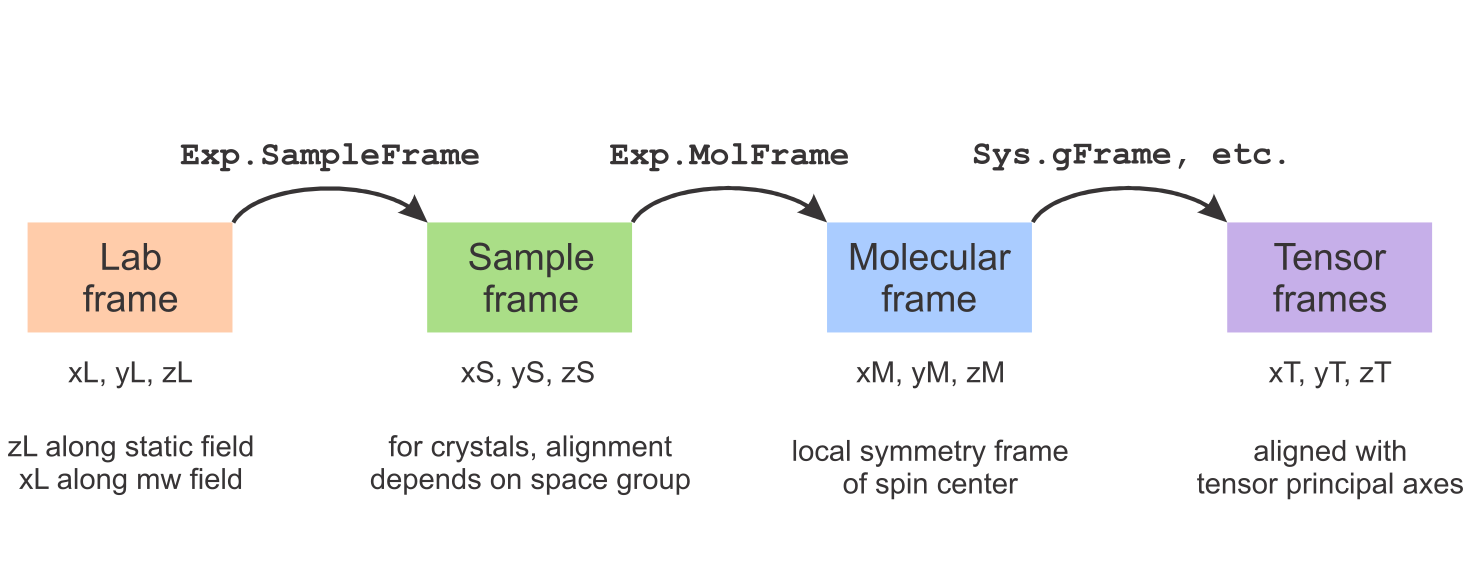
This overview explains at how these frames are defined in EasySpin and shows how you can specify the relative orientations between them. All frames are right-handed cartesian with orthonormal axes.

• Lab frame
• Sample frame
• Molecular frame
• Tensor frames
• Tensor orientations within the molecule
• Molecule orientation within the sample
• Sample orientation within the spectrometer

The lab frame L is fixed in the laboratory. Its three unit vectors are denoted xL, yL, zL. EasySpin defines the three axes of the lab frame as follows:

• zL is along the static magnetic field B₀, in agreement with the universal convention in magnetic resonance. For an electromagnet with horizontal B₀, zL is horizontal and points to the left. For a standard superconducting magnet with vertical B₀, zL is vertical and points up. For a split-coil superconducting magnet with horizontal B₀, zL is horizontal and points to the left.
• yL points away from the user.
• xL is defined such that the (xL, yL, zL) coordinate frame is right-handed. For an electromagnet, xL is vertical and points up. For a standard superconducting magnet, xL is horizontal and points to the right.

The following figure illustrates this.

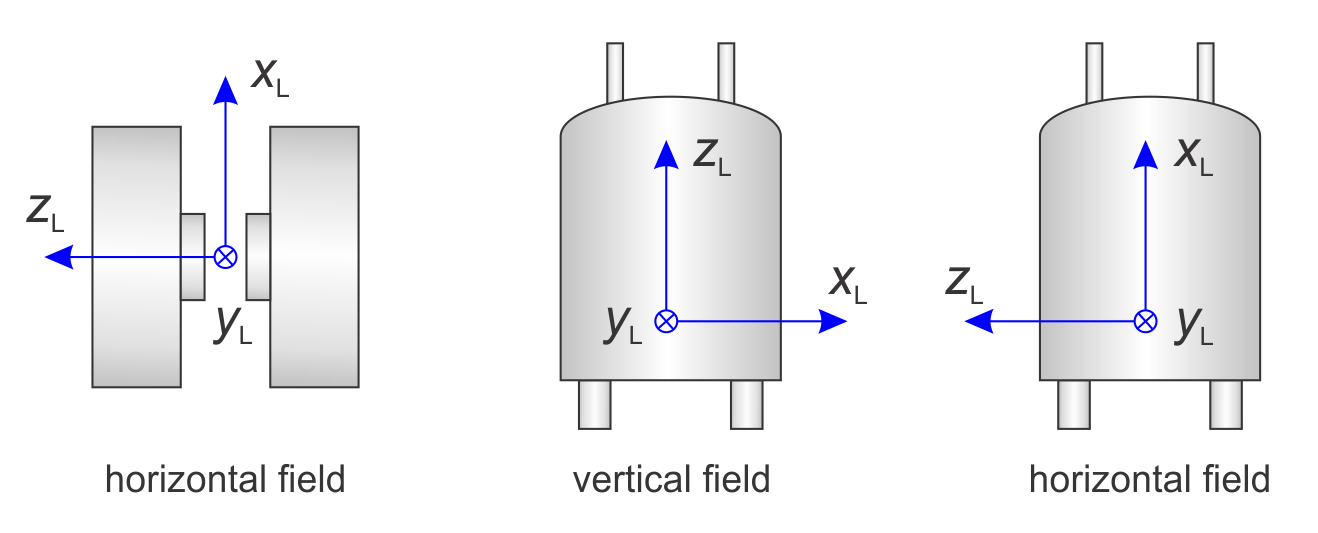
By default, the B₁ field of the incident microwave excitation is along xL for the standard perpendicular-mode resonators. For parallel-mode resonators, B₁ is along zL. You can specify non-standard mirowave excitation geometries using Exp.mwMode.

For photoexcited samples, the incident optical excitation beam (from a laser) is assumed to travel along yL by default, which is the common setup used with electromagnets. To specify other laser excitation geometries, use Exp.lightBeam.

The sample frame S is a sample-fixed frame with orthonormal unit vectors xS, yS, zS. The sample can be a crystal, a film, a frozen solution, etc.

In the case of a crystal, EasySpin follows the conventions prevalent in X-ray crystallography where the axis convention depends on the space group of the crystal:

• 1-2 (triclinic; point groups C1, Ci=S2): xS, yS and zS are arbitrary.
• 3-15 (monoclinic; point groups C2, Cs=C1h, C2h): For short Hermann-Mauguin symbols (like P2, Cm, P21/m, etc), yS is along the unique axis. For full Hermann-Mauguin symbols (like P211, P121, P112, etc), the space group symbol defines the unique axis (P211: xS, P121: yS, P112: zS, etc). In all cases, the other two axes are arbitrary.
• 16-74 (orthorhombic; point groups D2, C2v, D2h): xS, yS and zS are along the three two-fold axes. The assignment is arbitrary.
• 75-88 (tetragonal; point groups C4, S4, C4h): zS is along the four-fold axis. xS and yS are arbitrary.
• 89-142 (tetragonal; point groups D4, C4v, D2d, D4h): zS is along the four-fold axis. xS is along one of the two-fold axes.
• 143-148 (tetragonal; point groups C3, C3i=S6): zS is along the three-fold axis. xS and yS are arbitrary.
• 149-167 (trigonal; point groups D3, C3v, D3d): zS is along the three-fold axis. xS is along one of the two-fold axes.
• 168-176 (hexagonal; point groups C6, C3h, C6h): zS is along the six-fold axis. xS and yS are arbitrary.
• 177-194 (hexagonal; point groups D6, C6v, D3h, D6h): zS is along the six-fold axis, and xS is along one of the two-fold axes.
• 195-206 (cubic; point groups T, Th): xS, yS and zS are along the three two-fold axes. The assignment is arbitrary.
• 207-230 (cubic; point groups O, Td, Oh): xS, yS and zS are along the three four-fold axes. The assignment is arbitrary.

For crystal simulations, it is important to be aware of these conventions, as EasySpin relies on them to compute the orientations of all sites in the unit cell of a crystal given the orientation of a site in the asymmetric unit.

For partially ordered samples such as thin films, lipid bilayers and liquid crystals, xS, yS, and zS are arbitrary. One possibility that is often convenient is to define the zS axis to be perpendicular to the plane of the film or bilayer, or along the alignment direction of the liquid crystal.

For powders and frozen solutions, the definition of xS, yS and zS is also arbitrary.

In versions of EasySpin prior to 6, the sample frame was called crystal frame, and the axes were denoted as xC, yC and zC.

The molecular frame M is a reference frame that is fixed in the molecule or paramagnetic center. Its three unit axes are denoted xM, yM, and zM. You are free to choose the orientation of the molecular frame within the molecule, but it is best to follow existing conventions or align it with the local molecular symmetry. For example, put the zM axis along the plane normal of an aromatic radical or a planar transition metal complex. For a nitroxide radical, xM is conventionally along the N-O bond, and zM is perpendicular to the C-NO-C plane.

If you import data from quantum chemistry programs like ORCA, then you can take the frame from those calculations as the molecular frame. All imported atom coordinates and calculated tensors will be defined in this frame. EasySpin can import ORCA calculation results.

Last, there are the tensor frames T, with unit vectors xT, yT, zT. There is one frame for each tensor in the spin Hamiltonian, such as g, A, D, and Q tensors, as well as the rotational diffusion tensor. The tensor frame for a given tensor is its eigenframe. Its axes are aligned with the principal axes of the tensor. The particular order of principal values, and therefore the assignment of the associated principal axes to xT, yT, and zT, is arbitrary and up to you.

Next, we look at how you can tell EasySpin about the relative orientations between these frames.

Many paramagnetic centers have some local symmetry. An aromatic molecule has a unique plane normal axis, and a square-planar transition metal complex has a four-fold symmetry axis perpendicular to the plane. For such a center, atomic coordinates and tensor orientations are best expressed in a coordinate reference frame that aligns with these local symmetry elements. However, any molecule-fixed frame can be chosen as a reference frame. This coordinate frame is the molecular reference frame, or molecular frame for short. The corresponding axes are labeled xM, yM, and zM.

The orientation of every tensor you specify in EasySpin is related to the molecular reference frame. If the tensor is fully aligned with the molecular frame, then it is enough to simply give the three principal values of the tensor

Sys.g = [2.0 2.1 2.2];

For EasySpin, this means that the tensor axes - let's call them xT, yT, and zT - align with the molecular frame. The first g principal axis xT, with the principal value 2.0, is along xM, the second (2.1, yT) is along yM, and the third (2.2, zT) is along zM.

If the tensor is tilted with respect to the molecular frame, you can specify the tilt in terms of three Euler angles that describe the transformation from the molecular frame to the tensor frame (M→T). For a g tensor, specify this in the field Sys.gFrame. Here is an example:

Sys.g = [2.0 2.1 2.2];
Sys.gFrame = [30 27 81]*pi/180;  % Euler angles, molecular frame -> g frame

This means that to transform the molecular frame (M) to the g tensor frame (T), you first rotate the molecular frame by 30 degrees around zM, then by 27 degrees around the resulting y axis, and then by 81 degrees around the resulting z axis. It's important to realize that you rotate the frame, and not the tensor. The tensor stays untouched.

This works similarly for the other tensors. For hyperfine tensors, use Sys.AFrame, for zero-field tensors Sys.DFrame, for quadrupole tensors Sys.QFrame, for electron-electron interaction tensors Sys.eeFrame, for chemical shielding tensors Sys.sigmaFrame, and for nucleus-nucleus interaction tensors Sys.nnFrame.

If you want to get the coordinates of the tensor principal axes in molecular frame coordinates, use the following:

Sys.gFrame = [30 27 81]*pi/180;   % Euler angles for M->T transformation
R_M2T = erot(Sys.gFrame)          % matrix for M->T transformation

R_M2T =
   -0.3731    0.9251   -0.0710
   -0.8404   -0.3045    0.4484
    0.3932    0.2270    0.8910

The first row is xT, the second one is yT, and the third one is zT, all expressed in the molecular frame:

% tensor axes in molecular coordinates
xT_M = R_M2T(1,:).';
yT_M = R_M2T(2,:).';
zT_M = R_M2T(3,:).';

Vice versa, the first column is xM, the second column is yM, and the third column is zM, all expressed in the tensor frame.

% molecular axes in tensor coordinates
xM_T = R_M2T(:,1);
yM_T = R_M2T(:,2);
zM_T = R_M2T(:,3);

In many crystals, the spin centers do not align with the crystal axes. In these situations, it is necessary to specify a tilt between the sample frame (S), which is fixed relative to the crystal, and the molecular frame (M), which is fixed relative to the spin center. Use Exp.MolFrame for this. This field takes a set of three values that specify the Euler angles (in radians) for the transformation of the sample/crystal frame to the molecular frame (S→M).

Exp.MolFrame = [33 12 -76]*pi/180;  % Euler angles for S->M transformation

This means that to transform the sample/crystal frame (S) to the molecular frame (M), you first rotate counterclockwise by 33 degrees around zS, then by 12 degrees around the resulting y axis, and then by -76 degrees around the resulting z axis. Again, this transforms the frames, but leaves the physical objects (sample and molecule) untouched.

To get the vectors xM, yM, zM expressed in sample frame coordinates (we'll denote these as xM_S, yM_S, zM_S), use erot to calculate the corresponding transformation matrix:

a_S2M = [33 12 -76]*pi/180;  % Euler angles for S->M transformation
R_S2M = erot(a_S2M)          % corresponding transformation matrix

R_S2M =
    0.7269   -0.6849   -0.0503
    0.6642    0.7198   -0.2017
    0.1744    0.1132    0.9781

The three columns give the sample/crystal axes as vectors expressed in molecular-frame coordinates.

% sample/crystal axes in molecular coordinates
xS_M = R_S2M(:,1);
yS_M = R_S2M(:,2);
zS_M = R_S2M(:,3);

The three rows give the molecular axes vectors expressed in sample/crystal frame coordinates.

% molecular axes in sample/crystal coordinates
xM_S = R_S2M(1,:).';
yM_S = R_S2M(2,:).';
zM_S = R_S2M(3,:).';

To describe the orientation of a sample (crystal, film, etc.) in the spectrometer, you need to provide the relative orientation between the lab frame and the sample frame. For this, use the field Exp.SampleFrame. This field takes a set of three values that specify the Euler angles (in radians) for the transformation of the lab frame to the sample frame (L→C).

Here is a simple example.

Exp.SampleFrame = [30 45 -10]*pi/180;   % Euler angles for L->C transformation

This indicates that the lab frame (xL,yL,zL) has to be rotated by 30 degrees around its zL axis, followed by a rotation by 45 degrees around the resulting new y axis, followed by a -10 degree rotation around the resulting z axis, to bring it into overlap with the sample frame (xS,yS,zS).

Exp.SampleFrame describes the lab-to-sample frame transformation (L→S). In order to find the Euler angles for the reverse transformation, from the sample to the lab frame (S→L), invert the order and change the signs of the angles. Here is an example:

a_L2S = [72 15 -108]*pi/180;      % angles for sample -> lab frame transformation
a_S2L = [+108 -15 -72]*pi/180;    % angles for corresponding lab -> sample frame transformation

Exp.SampleFrame = a_L2S;          % EasySpin expects a lab -> sample frame transformation

To find out how the sample axes lie in the spectrometer, or how the lab axes lie relative to the sample frame, use EasySpin's erot to get the associated transformation matrix. Here is an example:

a_L2S = [10 45 0]*pi/180;                % Euler angles for L->S transformation
Exp.SampleFrame = a_L2S;
R_S2L = erot(Exp.SampleFrame)            % corresponding transformation matrix

R_S2L =
    0.6964    0.1228   -0.7071
   -0.1736    0.9848         0
    0.6964    0.1228    0.7071

In this matrix, the three columns are the three lab axis vectors xL, yL, zL, represented in sample coordinates. Conversely, the three rows are the sample axis vectors xS, yS, zS, represented in lab coordinates.

% columns: lab axes in sample coordinates
xL = R_L2S(:,1);
yL = R_L2S(:,2);
zL = R_L2S(:,3);

% rows: sample axes in lab coordinates
xS = R_L2S(1,:).';
yS = R_L2S(2,:).';
zS = R_L2S(3,:).';

Prior to EasySpin 6, the relative orientation between lab and sample frame was defined in the field Exp.CrystalOrientation. To convert code containing this to Exp.SampleFrame, invert the order of the three Euler angles and flip their signs.

%Exp.CrystalOrientation = [-20 47 73]*pi/180;  % EasySpin 5 - obsolete!
Exp.SampleFrame = [-73 -47 20]*pi/180;         % EasySpin 6 and later